Convexity and homogeneity are crucial properties of Gömböc. Weebles are straightforward examples of inhomogenous objects with Gömböc-type behaviour. Similarly, it is easy to create homogenous but concave Gömböc-like forms due to the fact that concave bodies cannot roll on all points of their circumference.

Shapes with a unique stable equilibrium are called monostatic; those with only one additional unstable point are referred to as mono-monostatic. Thus the Gömböc is the first convex, homogenous, mono-monostatic object.

Concave Gömböc-type planar shapes

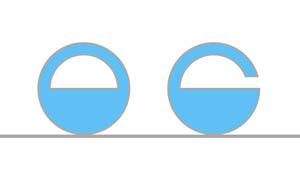
Planar Gömböc

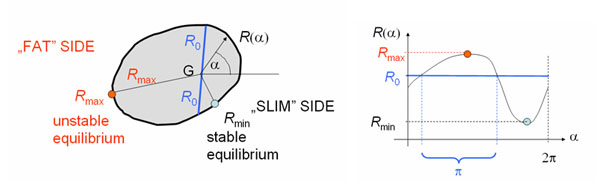
All planar, convex shapes can be defined by a function R(α) in a polar coordinate system with origin at the center of gravity of the object (G).

On horizontal surfaces, all objects start rolling in a way that sends G lower, i.e. such that R decreases at the point of contact with the underlying surface.

Equilibria occur if dR/dα = 0 at this point. A balance point is stable at minima of R (d2R/dα2 > 0) and unstable at maxima (d2R/dα2 < 0).

Minima of R are followed by maxima and vice versa, thus the numbers of stable and unstable equilibria are equal.  In addition, the following interesting statement can be proven:

Theorem 1:
All planar, convex, homogenous shapes have at least 2 stable and 2 unstable equilibria.
 
If an object had only one equilibrium point of each type, the diagram of the corresponding function R(α) would have just one maximum and one minimum.
The diagram R(α) diagram (left panel) and the corresponding body (right panel)

In this case one could cut it by a horizontal line R = R0 such that the two parts R > R0 and R < R0 of the function have equal (length π) horizontal projection.

This would correspond cutting the original object to a thin (R < R0) and a thick (R > R0) part by a line crossing the center of gravity G. Imagine supporting the planar object along this line. In order to maintain moment balance, G should be off the line, on the thick side, which is contradicts our previous statement that G is on the line.

Thus we arrived at a contradiction and therefore Theorem 1 is true.

As we have just proven, there is no planar, Gömböc-type object.

This surprisingly simple fact is the physical analogue of a classical mathematical theorem:

Four vertex theorem:

The curvature of a simple closed planar curve has at least four local extrema.

There are numerous generalizations of the Four vertex theorem as well as many related theorems in geometry, which are sometimes called Four vertex theorems together. If there were no Gömböc in 3D, this fact would be an additional member of the Four vertex theorem family.

Basic idea of the Gömböc

Similar to planar objects, 3D shapes can be defined by a function R(ϕ,ϴ) in a spherical coordinate system around their centers of gravity. 
Definition of a 3D shape in spherical coordinate system

Local minima and maxima of R again correspond to stable and unstable equilibria, but the object has additional balance points at saddles of R. According to the Poincaré-Hopf theorem the number of equilibria (s, u, t, respectively) of the three types satisfies s + u – t = 2 for all objects isomorphic to spheres. One could imagine three analogues of Theorem 1 (stating s>1 and u>1 for planar objects):

  • a) s > 1,
  • b) u > 1,
  • c) s + u> 2,

however  a) and b) are easy to confute:

s > 1 is not true as shown by this counterexample, for which s = t = 1, u = 2: 
 

There are simple counterexamples for i > 1, too. In this case, u = t = 1, s = 2:

The third possibility is the question of the Gömböc itself: are there 3D convex, homogenous bodies with s = u = 1 (thus t = 0)?

We can try to extend the planar proof to show the nonexistence of such bodies.

If there was such a shape, the corresponding function R(ϕ,ϴ) would have only one minimum and one maximum. The surface of the body could be cut by a level set R = R0 to a thin and a thick part of equal size (ie. the spatial angles determined by the two parts from G are of equal sizes).

If this level set is a planar curve (i.e. a circle), we get to contradiction, similar to the 2D case. However, it can also be spatial curve, as, for example, the curve on tennis balls. In this case, the separation of the body to an upper thick and a lower thin part does not mean that G has to be in the upper part. Thus, the planar proof does not apply in 3D.

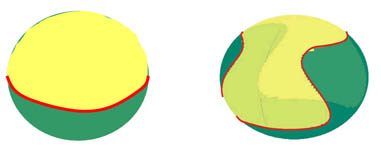
The line separating the thick (yellow) and thin (green) parts of a hypothetical mono-monostatic body can be, but is not necessarily planar

The ‘failure’ of the proof yields some idea for the shape of a spatial Gömböc. This idea was used to construct a two-parameter closed formula, for which it was analytically proven that appropriate parameter values result in an object with s = u = 1.

Unfortunately due to the additional constraint of convexity, the constructed form was almost identical to a simple sphere. Thus, this construction verified the existence of the Gömböc theoretically, but the existence of characteristic (visually obvious) mono-monostatic forms was still a question.

Some members of the two-parameter family of bodies used in the analytical proof

The ‘real‘ Gömböc

The ‘theoretical’ proof raised the question: why did we fail to get a characteristic shape? Either the formula constructed for the proof was not good enough or some deeper reason was hiding behind the failure.
 
The fact that Gömböc-type shapes proved to bear similar features to spheres and the lack of such shapes in a sample of 2000 pebbles at the island of Rhodes both suggested, that forms “far away” from the sphere can not have s = i = 1.
 
Nevertheless, using a different approach the real Gömböc could be constructed. The form presented below is based on the idea of the tennis-ball. It consists of segments of simple surfaces (cylinder, ellipsoid, cone) and planes.
 
The new shape is obviously convex. Numerical integration reveals that its center of gravity is slightly below the origin; this fact makes it easy to show that it is mono-monostatic.
 
Of course, infinite number of shapes have these properties, the figures show one of these. The fabricated Gömböc models are also slightly different: they consist of more segments, which makes the stability properties of the equilibria more robust and the dynamical behavior of the rolling objects more intuitive.
Simple segments are connected together to construct the Gömböc
The R=constant level curves of the Gömböc show clearly the tennis ball-shape

Related publications

Journal of Elasticity

Static equilibria of planar, rigid bodies: Is there anything new?

G. Domokos, J. Papadopulos, A. Ruina  •  36 pp. 59-66, 1994. 

  • proof of the nonexistence of the 2D Gömböc

Journal of Nonlinear Science

Static Equilibria of Rigid Bodies: Dice, Pebbles, and the Poincaré-Hopf Theorem

P. L. Várkonyi, G. Domokos  •  Vol 16: pp 255-281, 2006.

  • Theoretical proof of the existence of the 3D Gömböc.
  • Theoretical classification of shapes based on the number of their equilibria.
  • Classification of real pebbles- no Gömböc found.
  • The ‘Columbus algorithm’ proving the non-emptiness of all classes based on the existence of the Gömböc.
  • Relation between our two-dimensional theorem and the Four-Vertex theorem.

The Mathematical Intelligencer

My Lunch with Arnold

G. Domokos  •  28 (4) pp. 31-33, 2006.

  • Arnold and the conjecture of the Gömböc

The Mathematical Intelligencer

Mono-monostatic Bodies: The Answer to Arnold's Question

P. L. Várkonyi, G. Domokos  •  28 (4) pp34-38 (2006)

  • the real Gömböc
  • its relation to spheres
  • connection between the Gömböc and some turtles